6 . fejezet Folytonos valószínűségi változó

A 4. fejezetben események valószínűségének kiszámításával foglalkoztunk, majd az 5. fejezetben diszkrét valószínűségi változókkal. Amint azt láttuk, a gyakorlatban a véletlen kísérletek kimeneteleit számokkal jellemezzük, ezt a minden kimenetelhez egy számot rendelő függvényt valószínűségi változónak hívjuk és jellemzően \(X\)-szel jelöljük. A statisztikai változó fogalomhoz hasonlóan pl. \(Y\)-nal jelölünk egy további valószínűségi változót, vagy ha sok változóval dolgozunk a későbbiekben, akkor gyakori az \(X_1, X_2, \dots, X_k\) jelölés is. Fontos azonban megjegyezni, hogy -- bár nagyon hasonlók -- nem keverendő össze a 2. fejezetben megismert sokaságot leíró változó és a valószínűségi változó. Utóbbi egy absztraktabb fogalom, bár leírására hasonló fogalmakat is használunk majd, mint egy statisztikai változó esetén.

Attól függően, hogy a valószínűségi változó értékkészlete milyen számosságú, megkülönböztetünk a tananyagunkban:

• diszkrét
  • véges számosságú
  • megszámlálhatóan végtelen számosságú
• folytonos

valószínűségi változókat. A fenti besorolás nem teljes, vannak például vegyes eloszlások is, de ezeket nem tárgyaljuk.

A diszkrét valószínűségi változókkal ellentétben a folytonos valószínűségi változók jellemzően valamilyen mérési folyamat eredményeképp állnak elő, így a lehetséges értékek általában a nemnegatív valós számok valamely véges, vagy végtelen részhalmazán találhatók. Ennek megfelelően a folytonos valószínűségi változók kontinuum számosságú potenciális kimenettel rendelkeznek. Pontosan amiatt, mert a lehetséges értékek számossága nem megszámlálhatóan végtelen, az egyes elemi események valószínűségének szükségszerűen nullának kell lennie, azaz minden folytonos eloszlásra \(\mathbf{P} \left( X = x\right) = 0\) bármely \(x\) értékre.

A 6.1. ábra azt mutatja be, hogy ha végtelenül sűrűen helyezkednek el a lehetséges értékek egy intervallumon, és teljesül a \(\mathbf{P} \left( X = x\right) = 0\) feltétel, akkor a súlyfüggvény és az eloszlásfüggvény is folytonossá válik.

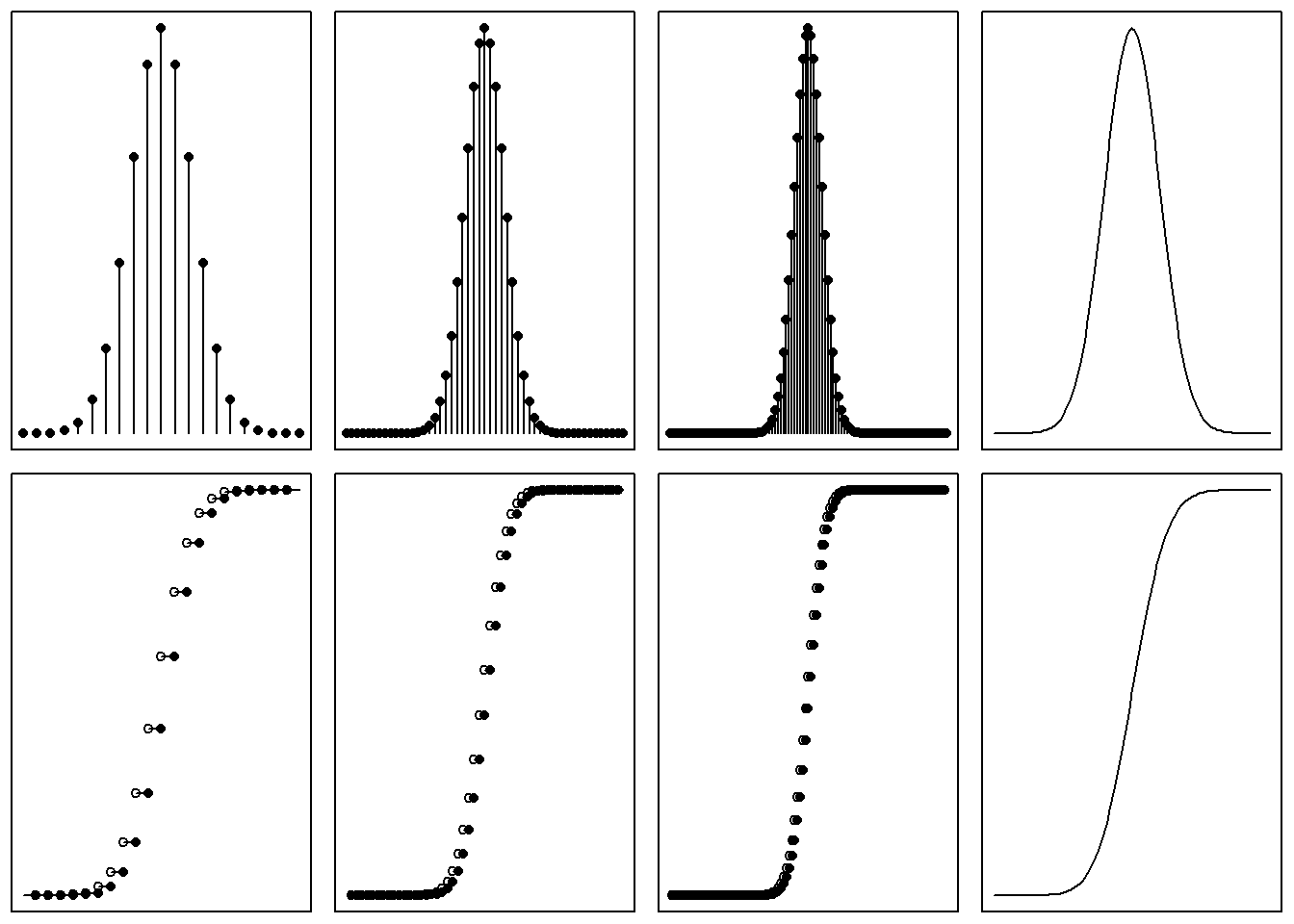
Ábra 6.1: Átmenet a diszkrét és folytonos valószínűségi változók között

A súlyfüggvény, amely definíció szerint a \(\mathbf{P} \left( X = x\right)\) valószínűséget adja meg diszkrét esetben, folytonos esetben értelmét veszti, a fentiek miatt. A súlyfüggvény helyett a sűrűségfüggvény fogalmát fogjuk bevezetni a következő alpontban, az eloszlásfüggvény szerepe azonban nem változik. Mivel tetszőleges valószínűség meghatározásában a sűrűségfüggvény közvetlenül nem, csak az eloszlásfüggvény segít folytonos esetben, ezért gyakran elsőként az eloszlásfüggvényt definiáljuk.